This physics brief was initially authored by Jason Jarvis in June 2013, has lead to other findings and was finally published officially here in this form on April 12th, 2019.
Reality physics, vacuum potential, the concept of a more perfect vacuum, lift, space propulsion advice, and the big bang never happened.
In order to explore and explain gravity mass momentum physics let's introduce the concept of a vacuum and space vacuum. In our daily lives we think of a vacuum as a suction machine.
An upright vacuum cleaner and a high capacity shop vacuum are 2 examples as they have electric motors that pull air through the geometry of the machine. As the electric motor runs it propels a fan to move air. This spinning fan acts like a pump and causes the air to move through it. With enough power and pleasing geometry the intake end of the vacuum cleaner can have significant vacuum suction which enables the machine to do its job of picking up the dirt or crumbs on the carpet.
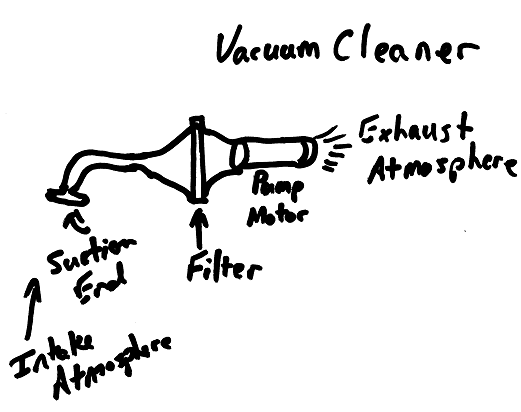
Figure 1: Illustration of a typical vacuum cleaner apparatus.
Vacuum or pressure can be measured and we can further illustrate the concept of a vacuum.
If you were to take an empty plastic bottle and use a suction technique to remove the air, for instance by inhaling with your lungs, the bottle would collapse due to the difference in pressure between the room and the bottle.
A simple collapsible plastic bottle is illustrated below. You could also seal an empty bottle with air at room temperature and witness the bottle shrinking in size after being placed in the freezer for a time. If you heated up the sealed bottle of air, the bottle would expand.
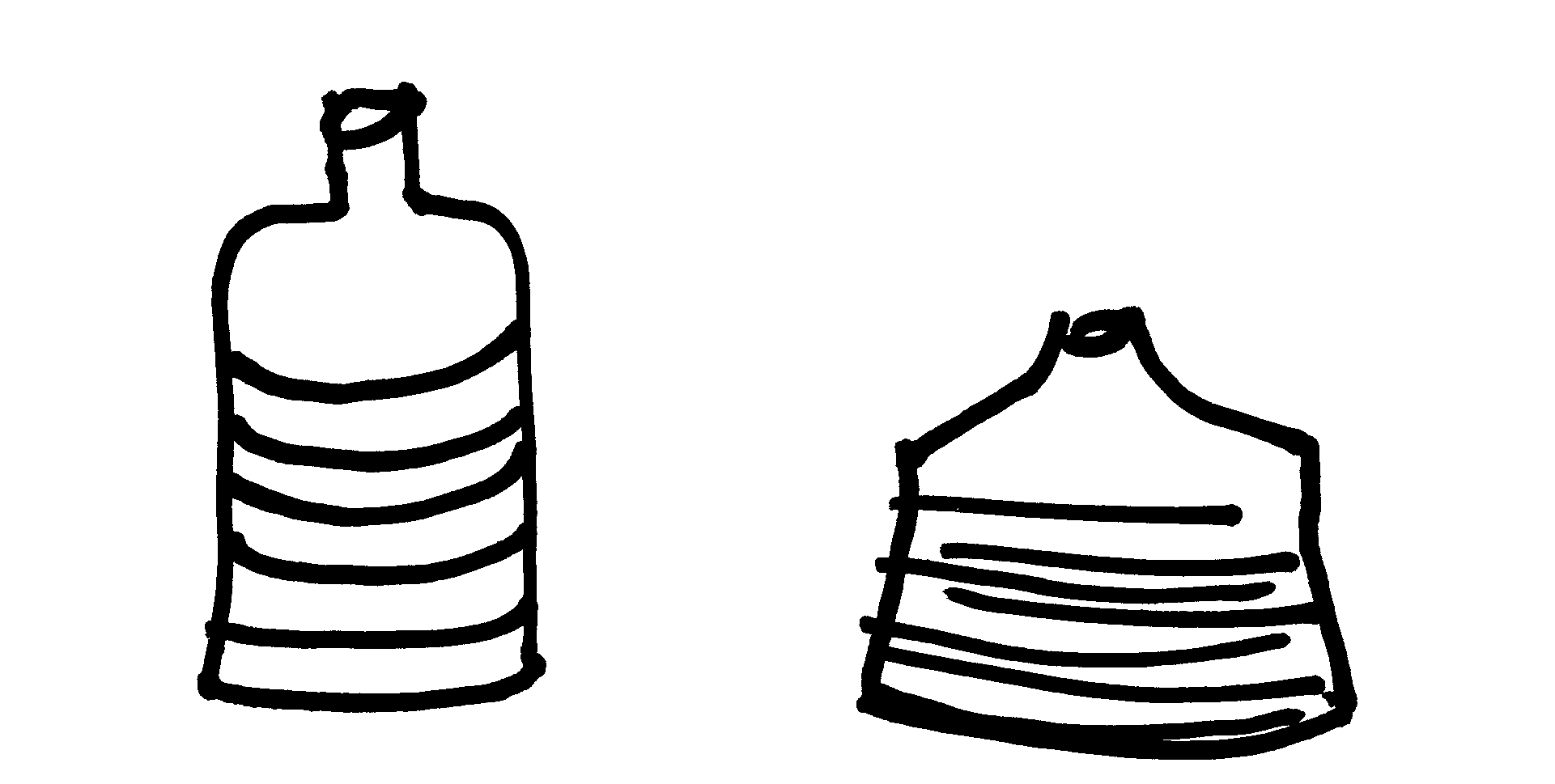
Figure 2: Vacuum explanation - using a simple plastic bottle an illustration of vacuum and pressure. You can pull the air out of the bottle causing it to collapse simply using your lungs.
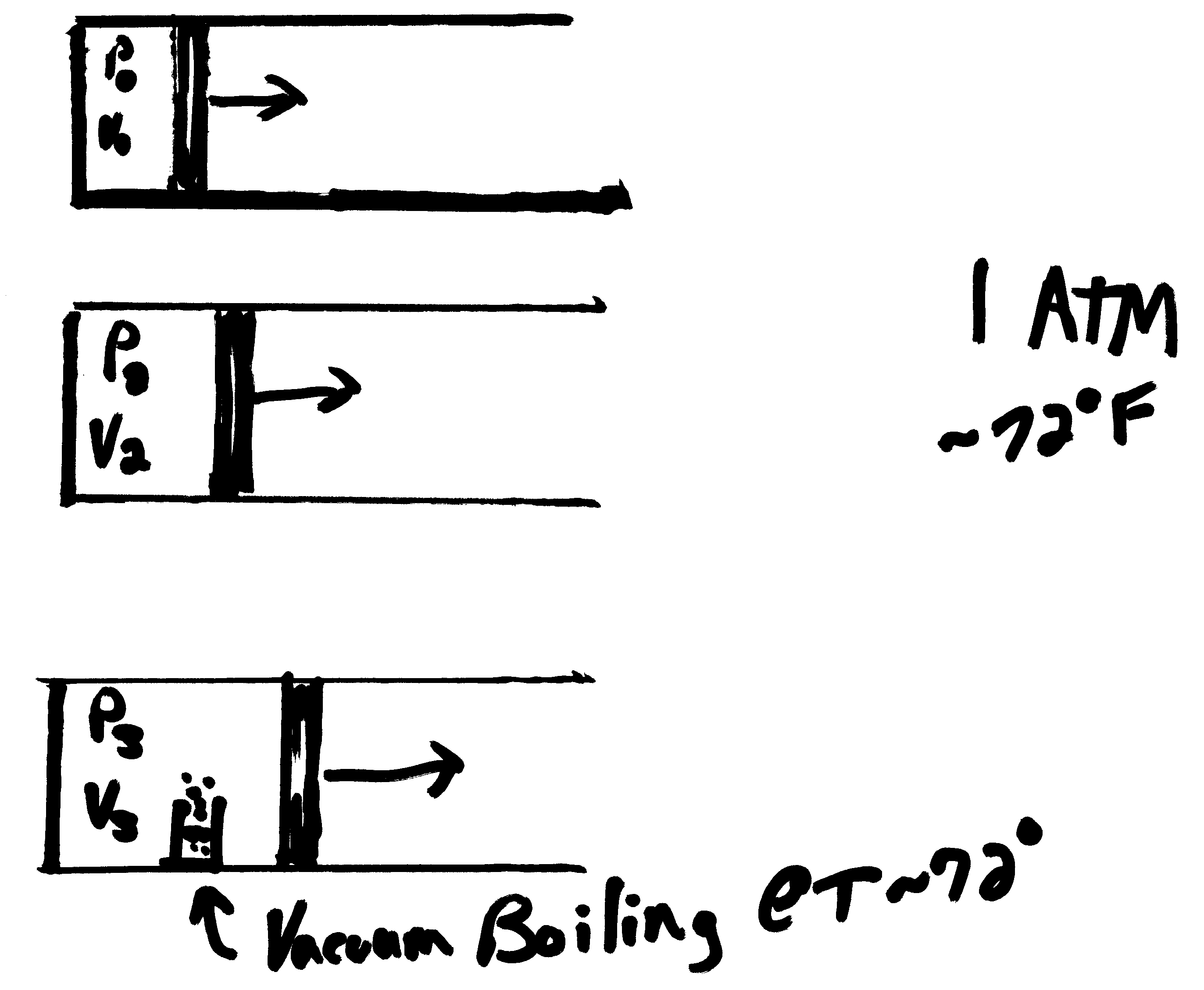
Figure 3: Vacuum explanation - piston and cylinder illustration by forcing the piston in you increase the pressure in the cylinder and by pulling the piston out or expanding you reduce the pressure. Illustration of vacuum boiling water at 72 degrees F.
Pressure and Vacuum Cylinder with Piston
Let's now consider a piston cylinder apparatus to further the discussion of a vacuum. If a volume of air is compressed the air pressure increases. If a volume of air is expanded the pressure decreases.
We know through ideal gas physics the relationships of pressure, volume, and temperature show that P1V1/T1~P2V2/T2. We also know that we can calculate the forces needed to hold the piston at steady state conditions as:
Pressure = Force/Area
and thus,
Force = Pressure*Area
Holding temperature constant 72° F (22.2° C) and using P1 at atmospheric pressure we can estimate the following P2, V2, and FPiston for the corresponding cylinder lengths.
| Chamber Length (m) | P2 | V2 | FPiston | ||
| 0.5 - compression | 202.7 kPa | 1.57 m3 | -318,322 N | ||
| 1 - equilibrium | 101.325 kPa | 3.14159 m3 | 0 N | ||
| 2 - expanse | 50.663 kPa | 6.28318 m3 | 159,161 N | ||
| 3 - expanse | 33.775 kPa | 9.42477 m3 | 212,214 N | ||
| 4 - expanse | 25.331 kPa | 12.566 m3 | 238,741 N | ||
| 10 - expanse | 10.132 kPa | 31.416 m3 | 286,489 N | ||
| 100 - expanse | 1.013 kPa | 314.16 m3 | 315,138 N | ||
| 1000 - expanse | 0.1013 kPa | 3141.6 m3 | 318,003 N | ||
| Using 1 meter radius Cylinder initial volume = Pi*r2*L initial cylinder length 1 meter | |||||
Table 1: Resulting pressure, volume, and piston force for a cylinder vacuum expanse
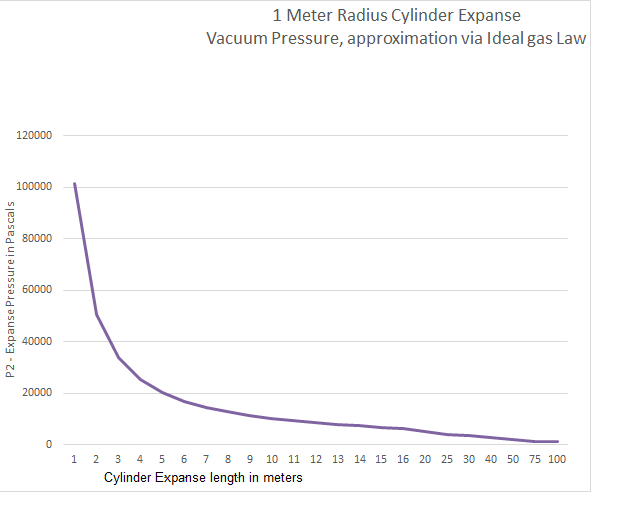
Figure 4: Charted estimate of 1 Meter Piston-Cylinder Expanse - using ideal gas law and discussion.
As you can see in the table above we can relate the new pressure in the chamber to the geometry and increasing volume of the cylinder. At a length of 2 meters the pressure in the vacuum cylinder is 1/2 the starting atmospheric pressure and the force required to hold the piston is ~159 kN (kilo-Newtons). With a long cylinder of 1000 meters the pressure of our 1 meter radius cylinder is 0.1013 kPa or 0.1 % of the initial cylinder pressure of 101.325 kPa. The piston force required to hold this position at 1000 meters is ~318 kN.
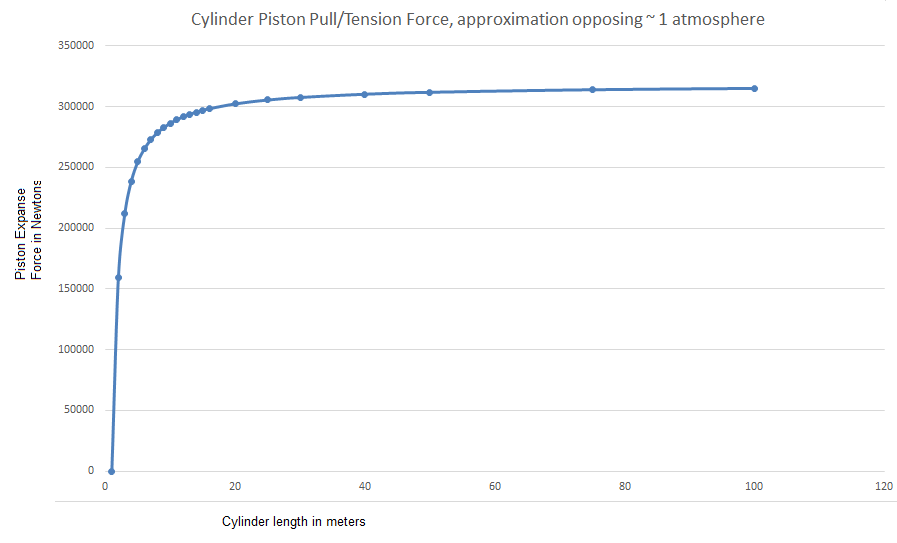
Figure 5: Charted estimate of cylinder piston force required to hold the piston at the new expanse cylinder lengths.
Standard Atmosphere Air is considered at 72° F (22.2° C) and 1 ATM, where standard atmospheric pressure of 101.325 kPa is used. The mass of air is generally given as water vapor in the form of relative humidity plus dry air. Dry air as we experience it here on Earth is comprised on Nitrogen, Oxygen, Argon, Carbon Dioxide, Hydrogen, Helium, and other trace gases. The density of air as a gas at 1 ATM and 72° F is ~ 1.3 kg/m3. The relative humidity adds mass in the form of water vapor to the total mass of air.
The composition of dry air is approximated by molecular weights as ~78% Nitrogen, ~21 % Oxygen, and the remaining 1 % contains the rest of the trace gases of the atmosphere. If we placed a glass of water in our vacuum cylinder chamber above we can see how water vapor behaves.
At V0 and P0, the glass of water remains liquid much as you would see it on the counter top in your kitchen at room temperature. We know that water boils at ~212° F (100° C). This is due to the vaporization pressure of liquid water. At 212° F, the vaporization point of liquid water equals the atmospheric pressure of the air around it and the water begins to actively boil. The time is takes for the water to boil is based on the volume and latent heat of vaporization while the boiling water stays at ~212° F until all the water is boiled off.
In our vacuum chamber we can make this water boil at a much lower temperature by decreasing the pressure of air around it to the vaporization point of water at that temperature. For 72° F (22.2° C) this pressure is ~ 3 kPa or in the case of our cylinder at about 30 meters long.
The table below illustrates the chamber pressure when the initial cylinder length is 1 cm. With a smaller initial volume the effective pressure is much lower in the chamber with respect to the cylinder length. In this case a pulled expanse to 1 meter cylinder length corresponds to a vacuum pressure of ~ 1,013 Pa or 1/100th of the initial atmospheric pressure.
| Chamber Length (m) | P2 | ||
| 0.01 - equilibrium | 101,325 Pa | ||
| 0.5 - expanse | 2,027 Pa | ||
| 1 - expanse | 1,013.25 Pa | ||
| 2 - expanse | 506.63 Pa | ||
| 3 - expanse | 337.75 Pa | ||
| 4 - expanse | 253.31 Pa | ||
| 10 - expanse | 101.325 Pa | ||
| 100 - expanse | 10.1325 Pa | ||
| 1000 - expanse | 1.01325 Pa | ||
| Using 1 meter radius Cylinder initial volume = Pi*r2*L initial cylinder length 1 cm | |||
Table 2: Vacuum expanse pressures using a piston cylinder with initial 1 cm length.
Geometric reference for approximating circles, cylinders, and spheres.
Area of a circle |
A = Pi*r2 |
Circumference of a circle |
C = 2*Pi*r |
Volume of a cylinder |
V = Pi*r2*L |
Surface area of a cylinder |
ASurface = 2*Pi*r2 + 2*Pi*r*L |
Volume of a sphere |
V = (4/3)*Pi*r3 |
Surface area of a sphere |
ASurface = 4*Pi*r2 |
Table 3: Geometric reference for circle, cylinder, and sphere.
In reality we use this piston cylinder physics everyday. The combustion engine uses compression and vacuum strokes of pistons and valves controlled by a camshaft and valve-train. Modern gas and diesel engines run with compression ratios from between 8:1 and 20:1 as the fuel mixtures follow the Carnot and Diesel cycles.
Vacuum pressure reference
| Pressure = Force/Area | 1 Pascal = 1 N/m2 | 1 lb-f =4.448 Newtons |
| Force = Pressure * Area | 1 ATM = 101325 Pa = 101.325kPa = 760 torr | 1 kg = 2.2 lbs |
| Density of Air = 1.3 kg/m3 | 1 torr = 133 Pascal | |
| P1V1/T1 = P2V2/T2 | Ideal Gas Approximation |
Table 4: Pressure and force relationships and units. Reference.
Vacuum chambers on Earth typically use another approach to creating a vacuum environment. Vacuum chambers are used in order to leverage the effect of a particle free environment as well as very low pressure scenarios.
A static tank or chamber is given plumbing, filters and pumps to draw the atmosphere air from its volume. As you can see below a illustration of a static chamber with a pump pulling a vacuum to the atmosphere.
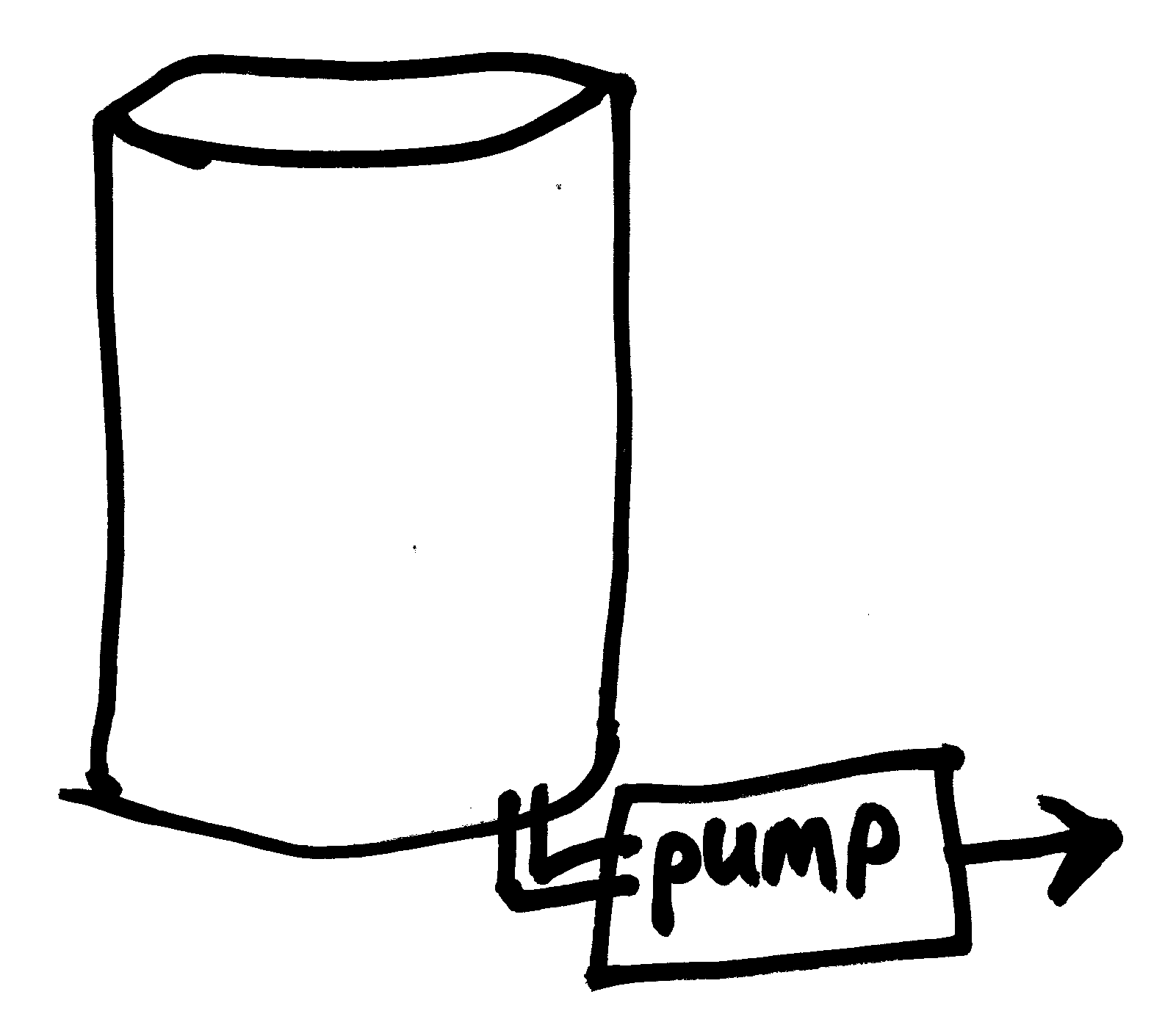
Figure 6: Vacuum explanation - Illustration of a vacuum chamber on in Earth atmosphere and a pump used to pull a vacuum in the chamber.
Vacuum Potential Thought Sphere
Let's now consider a vacuum physics thought sphere. As with the cylinder and piston example above we will conceptualize an initial spherical volume of air and discuss the physics as we expand the spherical surface area in a symmetricly spherical expanse chamber.
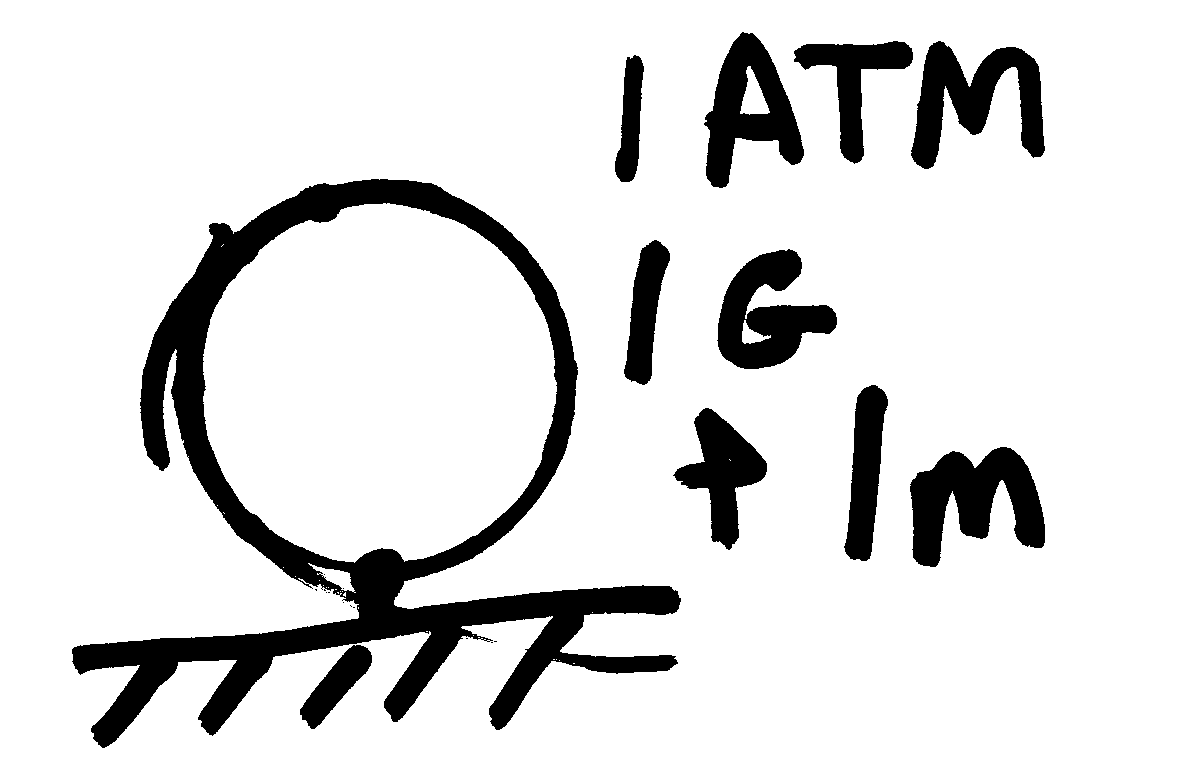
Figure 7: Vacuum Potential Thought Sphere - 1 Atmosphere of air illustration, 1 m radius, at atmospheric pressure
Our initial volume at V0 = 4.189 m3, based on a 1 meter radius, would contain at atmospheric conditions roughly 5.4 kg of dry air based on an air density of 1.3 kg/m3. At the initial volume and temperature of 72° F (22.2° C) the vacuum thought sphere stays at equilibrium with the internal and external pressures both being 1 atmosphere or 101.325 kPa.
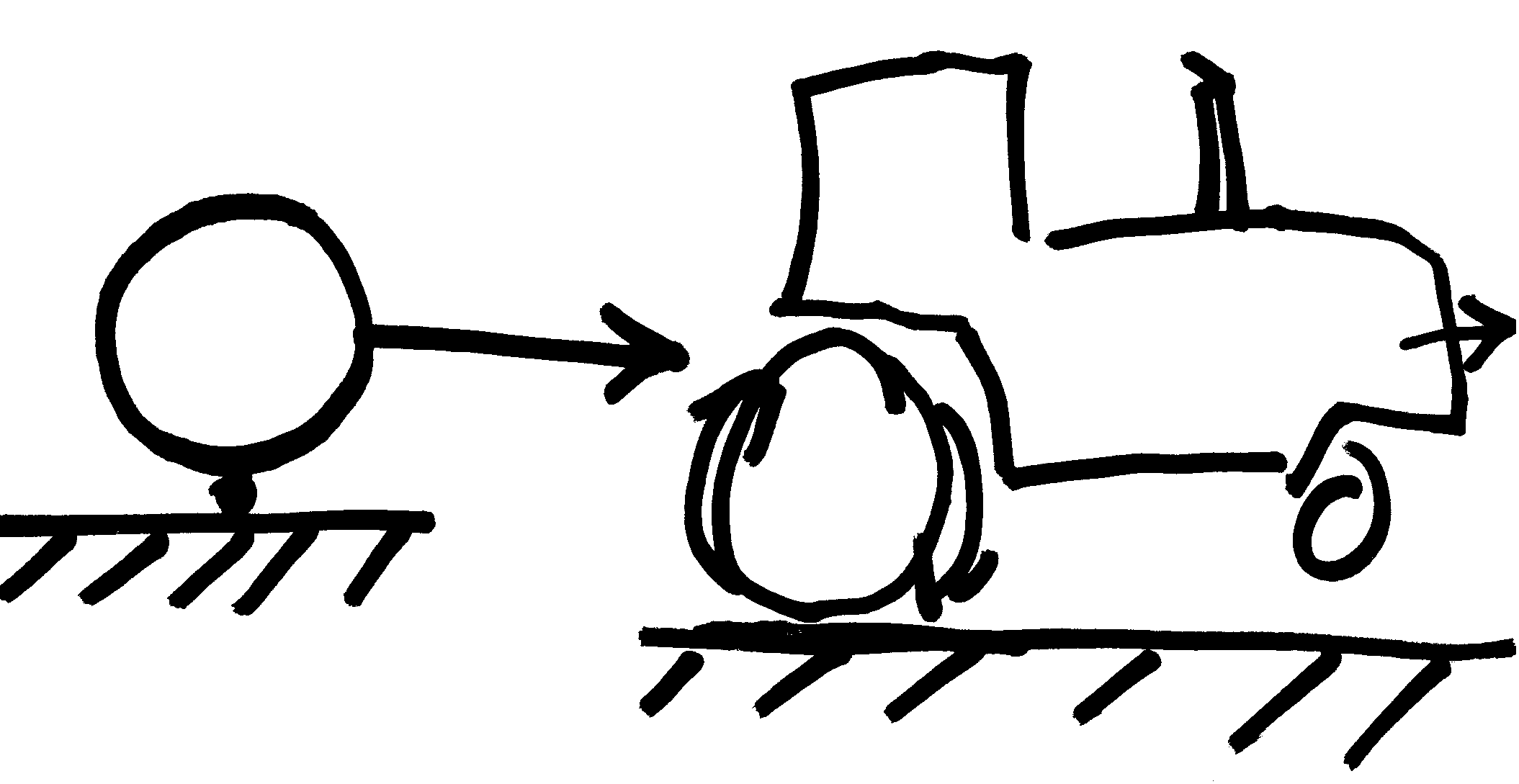
Figure 8: Vacuum Potential thought sphere - Much like the piston cylinder and vacuum chamber from above, this sphere has an expansive volume in order to reduce the internal pressure. The radius of this Vacuum potential thought sphere expands equally in all directions.
The vacuum expanse can be discussed using pressure physics with the ideal gas laws and we can see that as the volume grows the vacuum pressure inside changes much more dramatically for a sphere than with the cylinder example above. At a radius of 2 meters the vacuum pressure is 12.5% of the initial 1 ATM pressure at 1.2665 x 104 Pa or 95 torr. At a radius of 10 meters the internal vacuum pressure is now at 101.325 Pa and only 1/1000th of the original atmospheric pressure at 1 meter radius.
On the ground in 1g and 1 atmosphere we can take a moment to discuss internally what is happening to our air mass. You could experimentally apply heat, cooling, or even move the sphere along a path to correct and provide operating advice for this thought sphere. For now we will keep a simple discussion and know that we can both measure and apply thermal energy.
We can discuss what happens when we very rapidly or very slowly increase the vacuum expanse. So let's consider our thought sphere with an experimental setup where the radius is increased from 1 meter to several meters over a relatively short amount of time like 60 seconds. This time could be longer or shorter but for the moment let's revisit the original 5.4 kg of air.
Due to the increasing vacuum inside the thought sphere all the elements already in gas form would have more room to move about and the air inside would essentially want to fill the spherical space. Naturally due to the increasing radius and volume a pressure gradient in the sphere would be apparent. This pressure gradient would induce momentum to the air mass causing the air mass to form measurable velocities. The velocities of this gas would take on geometric swirling, due to sphere's geometry, becoming faster while this expanse is increasing.
Due to earth gravity at the current test site the air mass would most likely take on spinning and funneling motions with a vertically central form, akin to a water drain. Lighter elemental gases in the mix would find physical orientations above heavier elements.
Our tractor would then stop and hold the new expanse volume at V2, and we can now discuss what happens to the air mass momentum and swirls. The air inside would still be moving though as the volume has stopped expanding there is nothing to drive new momentum. Eventually, depending on the amount of work put into the system and the surface resistance of our thought sphere, the swirls would dissipate as the pressure gradients across the volume equalize. The entire volume could take on spinning but eventually at a steady V2 you can assess the new volume as a gaseous volume at lower pressure than V0.
With rapid vacuum expanse dynamics and the smallest of imperfections on the inner surface of the thought sphere there could be possibilities of vacuum/pressure eddies or vacuum snaps where small localized swirling events occur in the thought sphere. If an object were to be configured and positioned in the sphere, flow dynamics based on its location would be apparent.
It is easy to see a relationship of the tractor work to the momentum inside the thought sphere. You could also find evaporate effects where localized temperature gradients could be present.
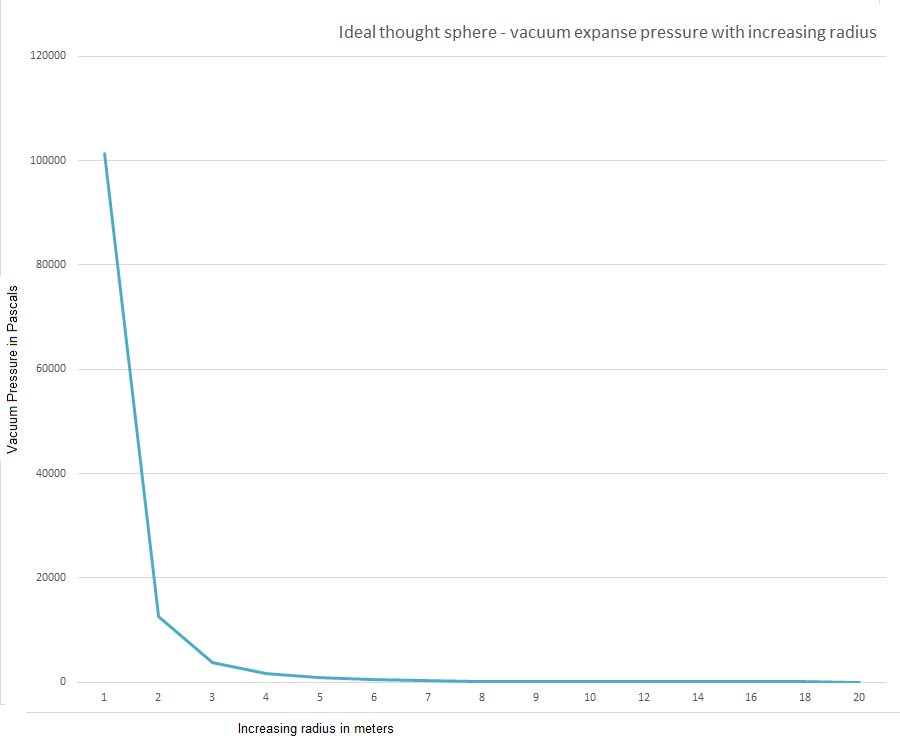
Figure 9: Ideal thought sphere to illustrate vacuum potential. Perfect spherical radius increase to decrease the pressure inside the sphere and oppose 1 atmosphere.
Below is a table illustrating the resulting vacuum pressures of a vacuum potential thought sphere. Theoretical vacuum pressures below are included for an expanse of up to 10,000 km in radius.
Spherical Radius in meters |
Volume in meters3 |
Vacuum Pressure in Pascals |
Vacuum pressure in Torr |
| 1 m | 4.1888 m3 | 1.01325 x 105 Pa | 760 torr |
| 2 m | 33.510 m3 | 1.2665 x 104 Pa | 95 torr |
| 10 m | 4,188.8 m3 | 101.325 Pa | 0.760 torr |
| 100 m | 4,188,790 m3 | 0.101325 Pa | 7.6 x 10-4 torr |
| 1,000 m (1 km) | 4.1888 x 109 m3 | 1.01325 x 10-4 Pa | 7.6 x 10-7 torr |
| 10,000 m (10 km) | 4.18879 x 1012 m3 | 1.01325 x 10-7 Pa | 7.6 x 10-10 torr |
| 100,000 m (100 km) | 4.18879 x 1015 m3 | 1.01325 x 10-10 Pa | 7.6 x 10-13 torr |
| 1,000,000 m (1,000 km) | 4.18879 x 1018 m3 | 1.01325 x 10-13 Pa | 7.6 x 10-16 torr |
| 10,000,000 m (10,000 km) | 4.18879 x 1021 m3 | 1.01325 x 10-16 Pa | 7.6 x 10-19 torr |
Table 5: Vacuum expanse modeled with a spherical thought sphere.
Swirling momentum as illustrated below in figure 10 can be manipulated with geometry and you could consider other gases such as heavy Xenon or light weight Helium. Also, based on mass momentum and the type of mass inside the thought sphere, there could be induced magnetic fields of varying strength. Due to very low vacuum pressures any mass would behave similar to when gas is super heated. Flows become very fast. Fluid and gas that is highly compressible will exhibit density gradients as well.
Figure 10: Vacuum Potential Though Sphere - The radius of this Vacuum potential thought sphere expands equally in all directions. Illustration of expanding vacuum chamber and vacuum thought sphere. Expanse causes air inside to gain swirling momentum.
Using the spherical surface area and the external and internal pressures we can determine the cumulative force required to hold the expanse of this sphere. We use the tractor illustration to signify this force required to maintain the vacuum expanse.
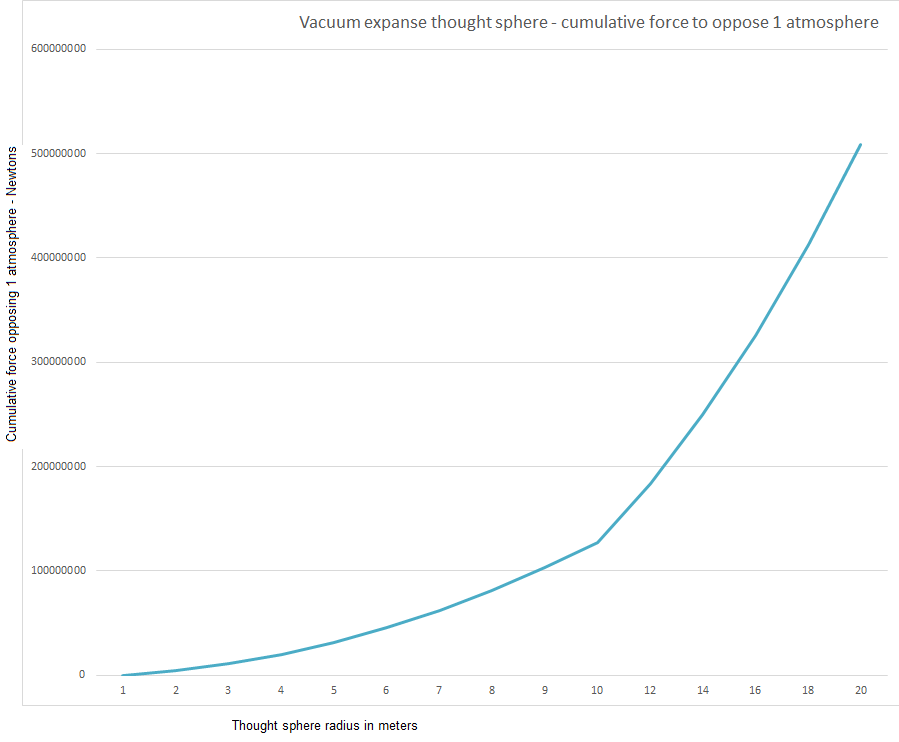
Figure 11: Ideal vacuum potential thought sphere chart showing the increasing cumulative force required to oppose 1 atmosphere with increasing radius in meters.
Spherical Radius in meters |
SphericalSurface Area in meters2 |
Vacuum Pressure in Pascals |
Cumulative internal Force due to pressure = InternalPressure X Area |
Cumulative External Force due to atmosphere pressure = ExternalPressure x Area |
Cumulative Force to hold Spherical Expanse |
| 1 m | 12.566 m2 | 1.01325 x 105 Pa | 1.2733 x 106 N | 1.2733 x 106 N | 0 N - V0 Equilibrium |
| 2 m | 50.265 m2 | 1.2665 x 104 Pa | 6.3664 x 105 N | 5.0932 x 106 N | 4.4565 x 106 N |
| 10 m | 1,256.6 m2 | 101.325 Pa | 1.2733 x 105 N | 1.2733 x 108 N | 1.272 x 108 N |
| 100 m | 125,660 m2 | 0.101325 Pa | 1.2733 x 104 N | 1.2733 x 1010 N | 1.2733 x 1010 N |
| 1,000 m (1 km) | 1.2566 x 107 m2 | 1.01325 x 10-4 Pa | 1.2733 x 103 N | 1.2733 x 1012 N | 1.2733 x 1012 N |
| 10,000 m (10 km) | 1.2566 x 109 m2 | 1.01325 x 10-7 Pa | 1.2733 x 102 N | 1.2733 x 1014 N | 1.2733 x 1014 N |
| 100,000 m (100 km) | 1.2566 x 1011 m2 | 1.01325 x 10-10 Pa | 1.2733 x 101 N | 1.2733 x 1016 N | 1.2733 x 1016 N |
| 1,000,000 m (1,000 km) | 1.2566 x 1013 m2 | 1.01325 x 10-13 Pa | 1.2733 x 100 N | 1.2733 x 1018 N | 1.2733 x 1018 N |
|
10,000,000 m (10,000 km) |
1.2566 x 1015 m2 | 1.01325 x 10-16 Pa | 1.2733 x 10-1 N | 1.2733 x 1020 N |
Table 6: Cumulative force to hold thought sphere opposed to 1 atmosphere.
Figure 12: Vacuum Potential Thought Sphere - Illustration at significantly larger radius. The radius of this Vacuum potential thought sphere expands equally in all directions. Illustration of expanding vacuum chamber and vacuum thought sphere.
The radius of Earth is averaged around 6,700 km, so we must now consider our vacuum expanse in space. If we were to move our thought sphere from the earth's atmosphere with the initial 4.189 m3 and 5.4 kg of atmosphere air the expanse would expand like a balloon due to the difference in internal pressure opposing a space vacuum. According to table 4 above the sphere with initial 1 atmosphere air would increase to a size of around 1,000 meters in radius to equalize pressure with a space vacuum of ~7.6 x 10-7 Torr. We would see that depending on the space vacuum around us our sphere would increase in size to meet the demands of deep space vacuum around it.
More Perfect Vacuum
Now we can introduce the concept of a more perfect vacuum. We now use our thought sphere to increase an expanse in any deep space vacuum or location to create a more perfect vacuum than the space around us. If we capture any initial volume of space and expand it we will have differences in pressure as seen above with similar needs for work to expand the thought sphere.
Figure 13: Vacuum Thought Sphere and the introduction of more perfect vacuum concept, theoretically we can increase the radius and create a more perfect vacuum than the space around it.
Expanse of the Universe Explained
Space, deep space, and planetary systems do not all have uniform vacuum pressures. Much like weather systems and fronts on earth, there are interactions at stellar scale between low pressure and lower pressure systems. As illustrated below if we create a release valve between a more perfect vacuum and space, the two vacuum pressures would equalize across the valve with very fast moving mass.
Space is not void of all mass. There is plasma gas forms of hydrogen, helium, and more than likely trace gases of most stable elements if you are given a large enough volume to analyze. Further if this volume were in a cold enough region of space you would find space dust, and ice, and ... This very concept is proof that aerodynamics and other fluid dynamic concepts can be employed for space vacuum and space travel.
As any two stellar systems interact the vacuum pressures between them will determine the speed and shapes of their mass interactions. Lower vacuum pressure systems likely have higher measurable speeds and orbits.
Figure 14: Vacuum Thought Sphere and the introduction of more perfect vacuum concept - with a more perfect vacuum than the space around it we could conceptualize a valve.
Planetary bodies that orbit a hot star such as the sun will naturally develop an expansion component to their orbits. Regardless of the gravitational attraction a planet has there will be a pressure difference between the sun facing and sun shaded side of the planet. Using Earth we have measured a difference in temperature between sun facing and shaded temperatures of around 200 degrees. This temperature reality results in vacuum pressure differences.
We could calculate a component of force away from the sun using this vacuum pressure difference. We can also determine orbital resistance for a body based on vacuum pressures in the region of space they find themselves.

Figure 15: Vacuum Potential and the Expanse of the Universe - As seen in this illustration the sun facing side and the shade side of a body in space have a significantly different temperature.
There is general speculation that cold dark regions of space have lower vacuum pressures than warm dense regions. It would naturally follow that the vacuum pressure in our own solar system decreases as you travel farther from the sun. True there are dense regions such as the Jupiter system, however a thought sphere at 5 AU and 39 AU would generally support this theory. This general concept can explain expanse of the Universe. Not all systems have the same operating conditions so we will find systems that expand faster than others.
Black holes are a very cold very low pressure vacuum system with very high momentum.
My speculation is that there is more matter or mass around a black hole than actually in a black hole. A black hole is actually a very fast moving mostly void vacuum of space dust. Mass is not drawn to a black hole due to gravity but rather sucked into a black hole by ever moving very strong vacuum. The reason that they appear black or dark is that any matter in them is moving so fast we can't see it. Mass that falls into a black hole will be orbited faster and faster towards the lowest pressure funnel spout. Large objects are continually broken down by faster smaller moving objects. As you approach the center objects are essentially all broken down into space dust or space plasma that is ever more accelerated by the vacuum pressure gradients. Finally this matter will reach an exit.
There will be strong pressure and temperature gradients between the outer limits of an accretion disk and the inner regions of a black hole. As we have detected the center exit spout or jet of a black hole will at times eject matter and other high energy particles.
This mass momentum reality will have gravitational consequences. As I have published before regarding Mass infinitesimal an observer would feel and see more mass moving in their direction than away from them. This is gravity mass momentum in play.
Just like anything else, no matter how fast your hot rod, someone will show up with something faster. Black holes and all stellar systems have a life cycle or are part of the over all life cycle of astrophysics. There will be larger, smaller, faster, and burnt out black holes. I could imagine dormant appearing black holes as a match ready to strike, or potentially jetting out cold ice rocks and space rocks.
Continuing with Gravity and Mass Momentum, on to Venus
Gravity, mass momentum, and the Super Rotation of Venus's Atmosphere
For the most current images of a black hole please see the event horizon telescope project.
https://eventhorizontelescope.org/
Also, see the official NSF site.
https://www.nsf.gov/news/special_reports/blackholes/
Other Vacuum potential realities will present themselves and the big bang never happened.
Vacuum Expanse Lift Discussion
While we are currently considering this vacuum expanse in Earth atmospheric pressure it is easy to point out lift due to buoyancy. Much like a helium filled balloon, our vacuum expanse is much lighter than the surrounding atmosphere.
| Spherical Volume radius | Volume - m3 | Mass Air Replaced | Vacuum Lift | Mass Helium | Helium Lift |
| in meters | in cubic meters | kg | Newtons | kg | Newtons |
| 1 | 4.188786667 | 5.445422667 | 53.36514213 | 0.749792813 | 46.01717256 |
| 2 | 33.51029333 | 43.56338133 | 426.9211371 | 5.998342507 | 368.1373805 |
| 3 | 113.09724 | 147.026412 | 1440.858838 | 20.24440596 | 1242.463659 |
| 4 | 268.0823467 | 348.5070507 | 3415.369097 | 47.98674005 | 2945.099044 |
| 5 | 523.5983333 | 680.6778333 | 6670.642767 | 93.72410167 | 5752.14657 |
| 6 | 904.77792 | 1176.211296 | 11526.8707 | 161.9552477 | 9939.709274 |
| 7 | 1436.753827 | 1867.779975 | 18304.24375 | 257.178935 | 15783.89019 |
| 8 | 2144.658773 | 2788.056405 | 27322.95277 | 383.8939204 | 23560.79235 |
| 9 | 3053.62548 | 3969.713124 | 38903.18862 | 546.5989609 | 33546.5188 |
| 10 | 4188.786667 | 5445.422667 | 53365.14213 | 749.7928133 | 46017.17256 |
Table 7: Exploring the concept of Vacuum and Helium lift via buoyancy in atmosphere. Vacuum lift is almost 16% more efficient than Helium balloon lift, using 0.179 kg/m3 for Helium density.