Momentum physics, lift, propulsion, and plume capture
Date: 11/19/2015
Some offline collected thought from Jason Jarvis
Good news Mars & Company. Momentum drive physics concepts to provide better propulsion techniques for the translation of motion of a craft through various means without the loss of propellant mass, concepts of plume capture by various centrifugal and non-centrifugal means, as well as lift and flight concepts enhanced by geometry and ∆T thus significantly increasing air transportation vehicle lift. As well as a technique of capturing all automobile exhaust emission for both increased engine efficiencies and the complete capture of Carbon.
------------------------------------------------------------------------------------------------------------------------------------------------------
I intend to show and prove that engineering, power, and mass momentum can be used to provide kinetic motion and thrust for position translation without the loss of propulsion mass in space.
Momentum
The momentum of a body in space is defined as its mass times its velocity vector based on a 3 dimensional point of reference. Below in equation form p is momentum, m is mass, and V3d is the velocity vector.
p = mV3d
The momentum of a system of particles can be summed by addition from a single point of reference.
psystem = m1V3d1 + m2V3d2 + m3V3d3 + ...
For a two body system the law of conservation of momentum mandates that the system momentum before the interaction and the system momentum after the interaction are the same.
Thus, Before After
m1V11 + m2V21 = m1V12 + m2V22
where, V11 and V21 are velocity vectors for m1 and m2 before the interaction while V12 and V22 are the velocity vectors for the masses after their interaction.
This provides the basis for propulsion physics and simplifies to one dimensional components in the thrust direction. Forces applied to bodies over a time interval change the momentum of the body. The change in momentum over this time frame is called the impulse. Thus propulsion.
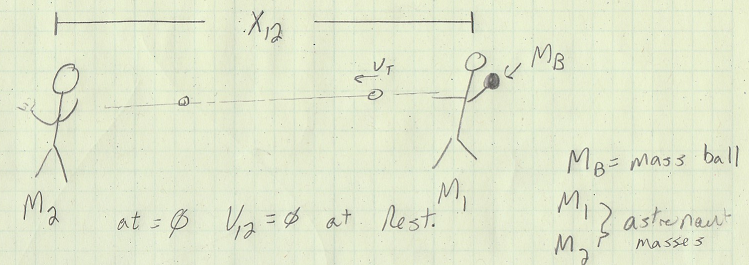
Figure 1: Hypothetical free floating Astronauts playing catch in space. Illustration of mass momentum conservation
Change in Momentum; Thrust and Propulsion Physics
Impulse: Throwing and catching in space, i.e. BASEBALL
Let's start by considering a situation where two astronauts are playing catch in space. These astronauts are geared up and initially start a distance of X12 apart and 0 velocity, i.e. V12 = 0. Astronauts each have a mass M1 and M2 and the ball has a mass MB.
Astronaut 1 faces astronaut 2 and throws a perfect pitch to astronaut 2. Assuming that his perfect pitch leaves his floating center of mass in a straight trajectory, astronaut 1 adds through conservation of momentum the equivalent of MBVB to his momentum away from astronaut 2.

Figure 2: Equation work for throwing the ball

Figure 3: Equation work showing the catch
Astronaut 2 on the other hand perfectly receives the pitch in his center of mass and absorbs the pitch's momentum of MBVB and starts to move away from the original at rest position frame adding to over all V12 away from astronaut 1
Astronaut 2 then fires a perfect pitch back to astronaut 1 at VB, thus adding MBVB to his momentum and increasing his velocity V2, adding to the total V12.
Astronaut 1 mean while moving at the speed of his first throw catches the ball perfectly along his mass centerline thus adding MB(VB-V12) to his momentum. Assuming our astronauts are trained to throw the same VB.
As you can see the Astronauts can ultimately keep playing perfect catch and propel themselves proportional to the mass of the ball and the speed of their throw. In our hypothetical space with no air resistance they can throw the ball far and keep going for a long time until V12 approaches the speed of their throw, at which time catching will take longer and longer.
Now let's consider air pressure. When throwing the ball on earth the primary forces acting on the ball are gravity (MBg) and air resistance when in flight.
Physics: Drag Force
Resistance due to air pressure is proportional to the velocity2 and has more effect the faster you go until you reach the what many refer to as the sound barrier. At this point the air volume ahead of it stacks up until you push through. For now we will use normal throwing speeds.
FDRAG= CDRAG (rho/2)V2A
FDRAG = drag force to resistance
CDRAG = the coefficient of drag
rho = air density
A = area of reference to the drag force

Figure 4: Illustration of resultant force due to air resistance with a ball velocity V

Figure 5: Illustration of playing catch on earth in gravity with air resistance
So we can model the baseball throw in space vacuum and in air with zero gravity. As the space air capsule illustrates below.

Figure 6: Illustration of hypothetical large air capsule floating in space - Throw path variance introduced by air resitance.
Now let's illustrate how we can propel a space ship conserving mass momentum and keep our baseballs.
To start with we will use a vertical model. This is for several reasons and simulated gravity in deep space will be due to geometrical circling and steady thrust.
If we start at rest in space the astronauts are floating in a gravity free cabin. Let's say we can artificially create a pressure gradient with either oxygen or inert artificial gas where the bottom or back of the ship has highest air pressure and the gradient from the top to bottom is slight but apparent. Also we can apply and maintain heat and cabin temperature gradients even slight.
Now we upgrade to a fixed perfect pitching machine so to transfer momentum from the throw to the ships forward motion.
Baseball Analogy for State physics and state change physics. Continue reading
Also, our baseballs our now engineered.
They start like a normal baseball so the astronauts can feed perfect pitches down the column into the lower chamber.
The balls immediately start to feel air pressure and wind resistance proportional to their velocity squared, but are moving toward the bottom of the ship fast off the pitching machine at VB.
These balls are enhanced with a trigger that is either electromagnetically or sensor tripped. Immediately their geometry pops into more of a gliding whiffle ball, same mass. As the ball pops out it may first catch a slight updraft and de-spin effect with the new air resistance profile. It then spirals down to bottom of the ship or in low gravity wobbles out and hovers to the bottom. The engineered effect is more like a leaf hitting the ground softly or a smooth airplane landing.
Can we agree that if the astronaut feeds the ball into the feeder and makes a perfect pitch through the pitching machine that MBVB is added to the ship's forward momentum? Can we also agree that if our engineering and cabin lengths are long enough the ball makes a landing where VB approaches zero, thus negligible negative momentum?
So how can we return the balls with zero lost forward momentum? If you were to float down the column and fetch a bag of balls you would have to kick off the other end with the weight of the balls creating a negative momentum effect, if would be canceled by your hitting the top side of the ship with the bag of balls.
Our balls are equipped with a return system. While at the bottom of the ship they were subjected to gradual electro warming and a gas bladder has expanded from a fold allowing each of the balls to gently float back across the man made temperature and pressure gradient with its very light heated gas providing the momentum efficient transfer.
Once they reach the top of the ship the astronauts simply pop them back into place and reset their switches. Then feed the pitching machine again. Obviously the length of the ship would need to be sufficient as well as the temperature and pressure gradient effects.

Figure 7: Engineered baseball to provide propulsion in hypothetical space ship, illustration of temperature, lift, and drag
Better pitch better catch, with an engineered football, illustration of some more physics concepts - bouyancy, ∆T and geometry, etc.
Let's consider a slightly different example with a momentum football as the propellant mass. We are also going to use water as the fluid and assume that at this point our ship has enough thrust to provide us with upright walking at FT <= 1 g on earth.
The footballs are heavy oblong looking objects. The inner core consists of a dense black grease looking substance at room temperature and are a heavy thermal viscous fluid. The black color is due to all the infused waste carbon.
The hard shell looking external housing is fixed width and slightly flexible length wise. The viscous core is packed in an engineered football housing between two end caps that are rigid in length from top to bottom and slightly flexible at its widths. The overall football shape and dimensions are experimentally optimized and engineered. There are spiral flow grooves on the outer surface.

Figure 8: Illustration of engineered momentum football, i.e. engineered propulsion mass, heavy thermal viscous core, internal gas pockets
These momentum footballs contain light gas buoyancy chambers which at cabin temperature would cause them to be buoyant and pointed down based on their internal gas chamber geometry at six feet deep in our water column given our hypothetical ships current simulated g-force.
These footballs are also equipped with magnetic or electromagnetic core caps so that we can electromagnetically accelerate them down the long water column as well as provide heat transfer to the internal gas pockets and thermal viscous core.
Let's assume the water column is engineered, big compared to the football and that the lower water bladder is also large enough such that localized cavitation and buoyancy are dominating. We may also use a salt gradient where the bottom of the column has the highest salt content and source. The furthest end of the exit bag is chilled.
Let's throw the football.
At the top of the ship a new trash mass is just off the compactor and has been bonded and balanced in its football shell. At cabin temperature the football is placed into the top water column pool that is 2 feet deep with a large funneling bottom. The football sloggy not soggy, due to its heavy mass and buoyancy, now makes it through the drop pool and comes out at 3 feet deep in the column, at this point it has one end up or the other based on the chambers and the elongated football geometry around its perceived center of mass.
Now between 4 and 6 feet deep you see the football start to take on a slow spin and disappear as a small stream of fine cavitation bubbles float up.
The footballs are accelerated down the length of the column, with increasing electromagnetic force cancelling buoyant forces. Due to the configuration of our gas chambers and football geometry they hold true form and balance. As they are pushed through the accelerator their core heats up. Our design and electromagnetic heat transfers give our balls even better buoyancy.
The footballs are then thrust through the exit of the column into the exit bladder. Once in the exit bladder they start to lose momentum in the negative, down, direction due to the dominating and increasing buoyancy force upward. If you were looking at the water column you would see the football come from nowhere, fast making a slight swirling arc from the center line. The football would swap ends base on our geometries, engineered inertial properties, and appear to bounce off an imaginary floor in the water column possibly in a swirling pendulum motion and with an arc back up the ball return channel.
If you have ever tried to swim a football or basketball to the bottom of the pool you know the effect of buoyancy. You can observe the pressure by the compression or flattening of the ball. You can observe the buoyant force as you try to keep it under, it is hard to push down. When you release an aired up ball from the deep end of the pool it rushes up and pops out if the water into the air. Its weight, air pressure, and volume determine how much upward momentum it will posses when it leaves the water surface. Needless to say at our column depth and charged buoyancy our footballs race back up the geometrically configured return chamber.
The buoyant force on an object is due to its density and volume compared to the fluid around it. The buoyant force is easy to measure in gravity and for our initial football scenario we have some to work with.
FBUOYANCY = density x g x Volume
Where, the apparent density uses the total mass and volume of the overall football apparatus.
As they race up to the top they have MBVB due to buoyant forces and are propelled with no negative momentum to the top of the ship. As they rise the force buoyant decreases, but they are still being accelerated fast enough to use them as an example of catching positive momentum.
The footballs are in the return column and still warm, very buoyant, and fast. We give them a target just below the water surface at the top of the column and they nail it transferring all of their MBVB to the ship's positive momentum. They then cool and are transferred to the drop column water pool.
Now our hypothetical ship needs to do a maneuver deep in space and needs to ramp up to a 5 g thrust. As the thrust becomes higher your balls buoyancy force is cancelled by the increasing g force, so a cold ball is buoyant at the same depth, 6 feet. In the exit stream your footballs start to make longer and longer exit arcs towards their imaginary bottom in the water column. The reason why they go further is the MV given to them makes their momentum carry them further until the buoyancy force slows them and sends it back up. The buoyancy return curve may look a little differently as well, however a deeper throw depth still brings back significant forward momentum on the ball return.
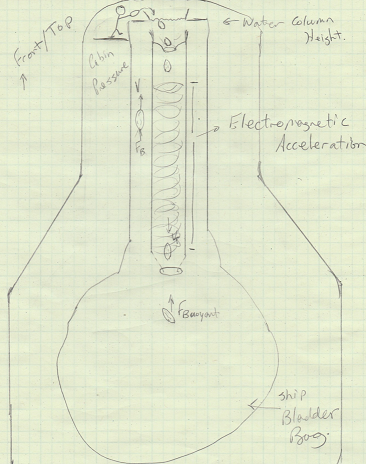
Figure 9: Hypothetical football mass momentum spaceship
Continue to Good News Mars and Company Part 2.
