Unlocking Jupiter, the Purpose of Gravity, and more discussion on Gravity Mass Momentum, continued analysis of Jupiter, the Great Red Spot, and its Moons
Published June 23, 2016, Authored by Jason Jarvis
Based on our previous discussions of Gravity, Mass, Momentum, Jupiter, and the introduction of Body N as a new planetary body we will now take a closer look at the Gravity Mass Momentum system around Jupiter.
Jupiter Facts and Comparison to Earth
Jupiter orbits approximately 5 times further from the sun than Earth and completes a solar orbit in 11.86 years. The gravity of Jupiter is estimated to be over 2.5 times Earth's gravity at 24.79 m/s2. We know that physically Jupiter is much larger than Earth. By volume Jupiter is estimated to be over 1300 times the size of Earth and the mass of Jupiter is 317 times that of Earth.
Jupiter Facts and Figures |
Earth Facts and Figures |
Earth Moon Facts |
|
Length of Day |
9.92496 hr | 24 hr | 655 hr rotation |
Approximate Radius at Equator |
69,911 km | 6,371 km | 1737.5 km |
Density |
1.326 g/cm3 | 5.513 g/cm3 | 3.344 g/cm3 |
Mass |
1.8981 x 1027 kg | 5.9722 x 1024 kg | 7.3477 x 1022 kg |
Assumed Surface gravity |
24.79 m/s2 | 9.80665 m/s2 | 1.624 m/s2 |
| Using Published Accepted data from NASA's Solar System and Planetary Facts | |||
Though Jupiter is so large it rotates on its axis as a Jupiter day in less than 10 Earth hours, ~9.92496 hr. This yields key evidence to mass momentum and gravity. We also know that the jet streams of Jupiter form distinct layers and velocities. We see the prograde upper jet streams moving faster than the planet spins. Jupiter's gravity is large enough and its mass momentum is fast enough to keep distinct flow separation all the way up to its upper atmosphere.
Jupiter spins so fast that centripetal forces are at play in Jupiter's internal makeup. As an example if an infinitesimal mass were to rotate about the equatorial middle of Jupiter in sync with the rotation it would be traveling at 12,300 m/s. Using the equatorial radius of 69,911 km, the centrifugal acceleration for an object moving at this speed and distance from the geo center of Jupiter would be approximately 2.162 m/s2. Thus its momentum would be countering Jupiter's gravity by almost 10%.
Let's expand on this concept of centrifugal acceleration to further model the gravity of Jupiter by exploring Jupiter's Moons.
Jupiter's Galilean Moons - Io, Europa, Ganymede, and Callisto
Galileo discovered the largest of Jupiter's moons in the early 1600's. These four moons are often referred to as the Galilean moons and are named Io, Europa, Ganymede, and Callisto. Using just their known orbit data we can begin to model the gravity of Jupiter.
As we see below using known orbital velocities (averages) and distance we can determine the centrifugal acceleration that is countering Jupiter's gravity. This acceleration is perpendicular to the orbit and along with Jupiter's gravity is responsible for keeping each orbiting moon on an apparently stable path. We discuss the eliptical orbits of moons later in the article.
Galilean Moons of Jupiter |
Io |
Europa |
Ganymede |
Callisto |
Orbit Velocity |
17,340 m/s | 13,743 m/s | 10,879 m/s | 8,203 m/s |
Orbit Radius about Jupiter |
421,800 km | 671,000 km | 1,070,400 km | 1,882,700 km |
| Using Published Accepted data from NASA's Solar System and Planetary Facts | ||||
| We are using averages for orbital characteristics and circular geometries for math | ||||
| Centrifugal Acceleration about Jupiter/ie V2/R, units in m/s2 | 0.7128164 | 0.281489 | 0.110572 | 0.0357413 |
If we take these acceleration calculations and plot them with respect to the distance from Jupiter's geometric center we see a trend unfolding.

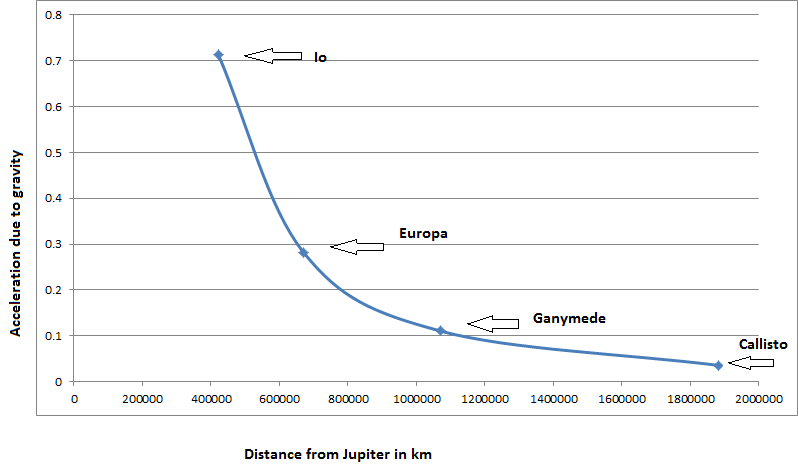
More discussion of Galilean Moons and their Orbits
As you can see from the 4-Moon illustration above at a distance of 421,800 km from Jupiter's geometric center, the Moon Io orbits in a much higher gravity field strength than its Galilean neighbors. The strength of the gravity field tapers off with respect to distance from the planets core.
We are currently modeling using gross and average numbers for orbital velocity and distance of these moons. This leads to simpler modeling using circular geometry. In actuality the Galilean moons have varying elliptical orbits. Each pass of Jupiter they speed up and slow down as they keep roughly an average stable orbit.
Until now the elliptical orbit of the 1st Galilean moon Io was thought to be induced by interactions and close passes with its neighbor moons. As you can see each of these moons do have an estimated gravity and they cannot ignore their neighbors, however the moon Io's elliptical orbit is mostly due to its exit and formation from Jupiter's core as a Body N. Io exited Jupiter's upper equatorial atmosphere and has essentially spiraled into its current position elliptically over time. Io feels the gravity interactions as well with Body N.
The moon Europa is the second Galilean moon from Jupiter at a distance of 671,000 km. The gravity attraction of Europa and Io at their current distances cannot be ignored and the system of moons appear to be lined up becoming new worlds. Ganymede orbits at near 1 million km while Callisto orbits at over 1.8 million km.
As you can see in the above illustration each moon feels less of Jupiter's gravity as you study the Four Galilean moons of Jupiter.
Expanding to include more of Jupiter's known Moons
Jupiter has many moons and satellites so let's add a few more interesting ones to our plot to see what the gravity trend looks like. As you can see below the inner moon named Metis orbits in a gravity field strength of 7.778 m/s2.
We consider the following 10 orbiting moons of Jupiter to expand our gravity trend plot and comparison. Jupiter moons Metis, Adrastea, Amalthea, Thebe, Io, Europa, Ganymede, Callisto, Themisto, and Himalia are detailed in this following table.
Jupiter Moon |
Metis |
Adrastea |
Amalthea |
Thebe |
Io |
Europa |
Ganymede |
Callisto |
Themisto |
Himalia |
| Orbit Velocity | 31,554 m/s | 31,480 m/s | 26,489 m/s | 23,905 m/s | 17,340 m/s | 13,743 m/s | 10,879 m/s | 8,203 m/s | 4,136 m/s | 3,304 m/s |
| Orbit Radius | 128,000 km | 129,000 km | 181,400 km | 221,900 km | 421,800 km | 671,000 km | 1,070,400 km | 1,882,700 km | 7,507,000 km | 11,461,000 km |
| Using Published Accepted data from NASA's Solar System and Planetary Facts | ||||||||||
| Acceleration m/s2 | 7.778 | 7.682 | 3.868 | 2.575 | 0.7128 | 0.2815 | 0.1106 | 0.03574 | 0.002279 | 0.0009526 |
When we plot more of Jupiter's moons on an acceleration versus orbit distance plot we see the gravity strength of Jupiter increase dramatically as it approaches ~24 m/s2 at the 69,911 km radius of the upper atmosphere.
The plot below illustrates the trend and shape of the gravity strength curve as you approach the upper atmosphere of Jupiter.
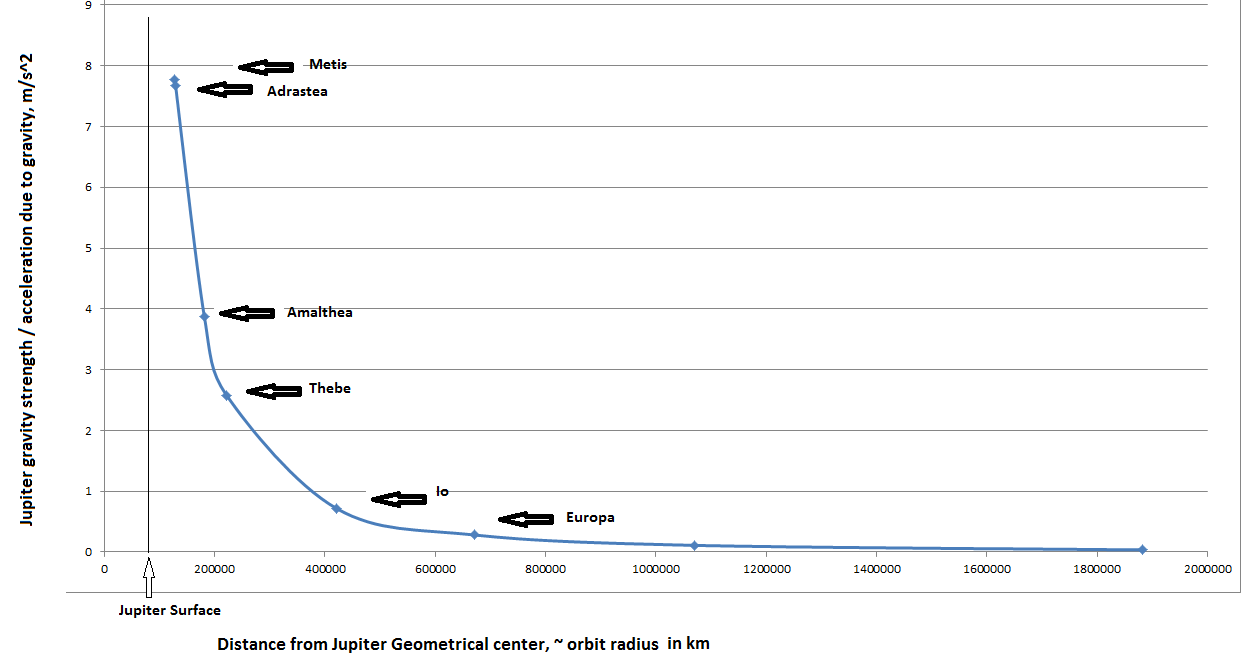
First Suggested model for Jupiter's acceleration due to gravity based on radius from geometric center
We have an idea for the relationship of gravity's strength due to distance. Essentially the closer you are to something the greater the attraction due to gravity. The acceleration plots and trends from above can be extended to provide a suggested gravity map of Jupiter from its geometric center.
We know from Earth data that the shape of the gravity strength curve falls the fastest once you leave Earth's upper atmosphere. The plot data from above shows this gravity strength and its rapid increase at it approaches the upper atmosphere at approximately 69,911 km.
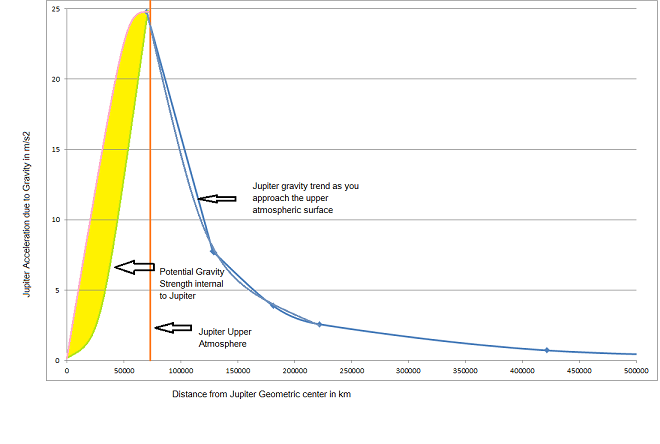
Modeling for the internal gravity of Jupiter may be modeled with a similar shape to the above plot. As you approach the geometric center or core of Jupiter the gravity begins to decrease as more mass becomes apparent around your infinitesimal test mass.
As your depth increases in the Jupiter atmosphere you will still find increasing pressures, heavier elements, higher temperatures, yet gravity is cancelling and becoming smaller. The pressure and weight of the upper atmosphere is a persistent pressure cap on the gaseous thermo fluid composition of Jupiter.
Gravity Field Magnitude of Jupiter compared to Earth
Jupiter is known to have 2.5 times the gravity of earth where earth has approximated gravity of 9.8 m/s2, Jupiter has an approximated gravity of 24.79 m/s2. Earth's acceleration due to gravity with respect to its radius can be examined in the Earth Moon relationship. By comparison Earth's gravity strength at the Moons orbit distance (384,400 km) is modeled at 0.0027191 m/s2.
As discussed previously the International Space Station orbits as a free fall satellite. The illustration shows the space station orbit velocity cancelling approximately 8.6 m/s2 of gravity at the ISS orbit altitude of approximately 400 km.
The illustration below shows Earth's acceleration due to gravity compared to Jupiter. We see that not only is the magnitude of Jupiter's gravity much higher, but also that the shape and distance of the gravity field is much larger.
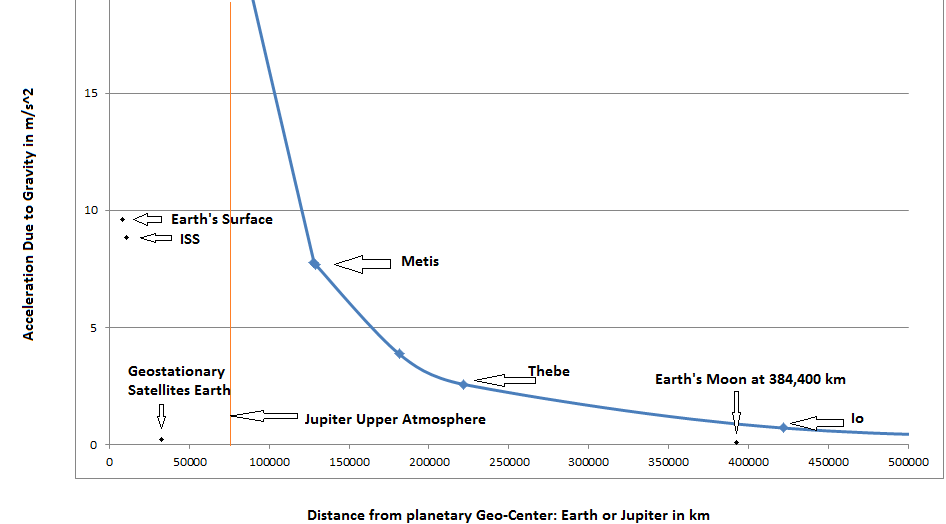
Chart above is a Jupiter Earth comparison from center of mass or radial from orbiting center of mass.
Jupiter Atmosphere and Thermo Fluid Composition
As of June 2016 Jupiter is believed to be comprised mostly of Hydrogen and is considered to be a large gaseous planet. The average density is estimated to be 1.326 g/cm3 while the density used for Earth is 5.513 g/cm3, 4 times higher. Though the density is much less than Earth, the overall size of Jupiter's atmosphere, much higher gravity, and momentums lead to large compressed thermo fluid flows.
A simple pressure model can begin to illustrates the effect of gravity and depth within Jupiter's atmosphere.
Atmospheric pressure depends on the density of the atmosphere, gravity, and depth. For Earth we experience 1 ATM at the surface and 1 ATM of pressure is defined to be 1.01 x 105 N/m2.
Simple pressure formula based on depth in a fluid
P = rho * g * D,
where rho is density of the fluid or gas, g is acceleration diu to gravity, and D is the depth.
Let's now use the estimated average density of Jupiter of 1.326 g/cm3 to determine the equivalent depth within Jupiter's atmosphere to create 1 ATM equivalent pressure. A simple calculation and solving for D (depth) gives us a depth of only 3.07 meters in Jupiter's atmosphere.
So we realize that the average density value would not be the best way to model Jupiter's upper atmosphere. The actual density of the planet varies with radius and we will find that the core of the planet is more dense than the upper atmosphere. For this upper atmosphere model we assume here a much lower density value for rho of .070 g/cm3 or 70 kg/m3. We know on Earth that the air gets really thin the higher you go into the atmosphere.
Potential Pressure Modeling of Upper Jupiter Atmosphere |
rho (density) | g (gravity) | D (depth) |
| 1.01 X 105 N/m2 -1 Atmosphere Earth | 1326 kg/m3 | 24.79 m/s2 | 3.07 m |
| 1.01 X 105 N/m2 -1 Atmosphere Earth | 70 kg/m3 Hydrogen | 24.79 m/s2 | 58.2 m |
| 1310 kpa - ~ 13 x Earth Atmosphere | 70 kg/m3 Hydrogen | 24.79 m/s2 | 756 m |
| 5.05 X 108 N/m2 ~ 5,000 x Earth Pressure | 70 kg/m3 Hydrogen | 24.79 m/s2 | 291 km |
As you can see from the table above even using the density of the lightest stable element of hydrogen at only .070 g/cm3, yields one atmosphere equivalent at a depth of only 58.2 meters. The critical point of hydrogen where liquid and vapor both exist is at a mere 756 meter depth. At depths greater than 756 meters there is a high potential for flowing liquid hydrogen and other light elements.
Jupiter's upper Jet Streams are flowing Rivers
The upper atmosphere that we see around the equator of Jupiter is as much a flowing river as it is a Jet Stream. These rivers at depths around the equator of Jupiter may contain flowing rivers of compressed H2O. Water is a stable combination of elements and the critical point for pressure of water is a mere 1200 x 1 ATM at a theoretical depth in Jupiter's atmosphere of only 70 km.
Jupiter has abundant Hydrogen and the opportunity for Oxygen is statistically high as a result of reactions lower in the atmosphere.
The temperatures of Jupiter are known to be cold in the upper atmosphere ~ -135 C or colder. Recent infrared data however shows a glowing internal core. With the pressures, gravity, and pure kinetic energy in the Jupiter atmosphere I would venture that the planet gets hot, 10's of thousands of degrees or hotter towards the core. With the above pressure modeling we see that the pressure is extreme at 5,000 x 1 ATM at a depth of only 291 km. 291 km is barely scratching the surface of Jupiter's equatorial radius of 69,911 km.
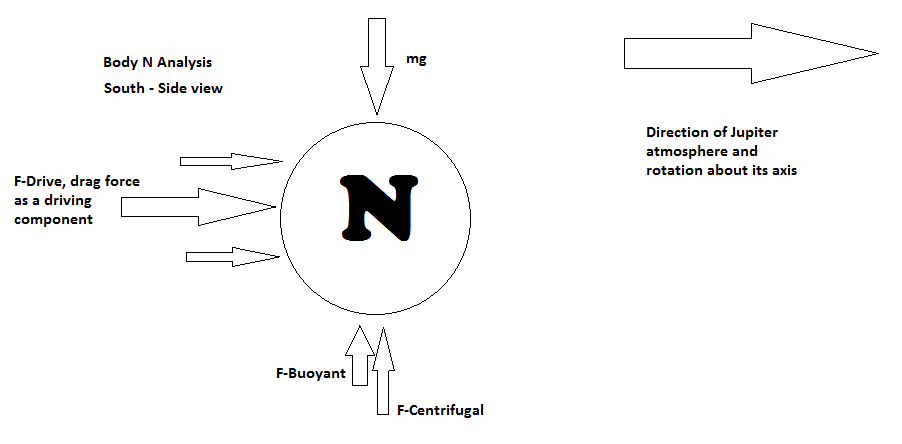
Body N Analysis, the Driving mechanism of Jupiter's giant storm
As previously introduced Body N is theorized to be the driver beneath the Great Red Spot of Jupiter. If the Great Red Spot is to be a result of Body N then its location must be somewhere beneath the spot. As mentioned in the introduction of Body N previously it is orbiting internally to Jupiter's atmosphere at roughly 9.92 hrs in sync with the planet. If we approximate a Body N distance from Jupiter's geo center of roughly 65,000 km, we would place our Body N at 69,911 - 65,000 ~ 5,000 km beneath the upper equatorial atmosphere. The corresponding centrifugal acceleration away from Jupiter's geometrical center can then be estimated and modeled.
Body N Altitude |
60,000 km | 65,000 km |
| Depth in Atmosphere | ~ 10,000 km | ~ 5,000 km |
| Approximate Velocity ~9.92 hr Jupiter day | 10,556 m/s | 11,436 m/s |
| Centrifugal Acceleration | 1.8573 m/s2 | 2.012 m/s2 |
Thus Body N has gravity canceling acceleration of ~ 2 m/s2 in the upper Jupiter atmosphere.
Regardless of the precise depth and velocity of Body N, the atmosphere of Jupiter is ever faster in the same prograde direction. As you see Body N has a significant tail wind which we can model similar to drag on a sphere. Drag force or in this case drive force for a sphere is dependent on the density of fluid, velocity2 of the fluid with respect to the body, and the exposed surface area to the flow.
There is also the potential for a significant buoyant force on Body N. The force due to buoyancy as we typically model it depends on gravity, the volume displaced, and density of the surrounding fluid.
Our Body N could have a much higher density than the surrounding upper atmosphere, however it will still have an extreme pressure difference between the lower and upper altitudes. Pressure is a significant reality as seen above in the depth pressure modeling.
The typical model for Buoyant force and a Large Body Pressure Model
FB ~ rho * g * VNVolume,
where rho is density of the fluid, g is Jupiter's gravity, and VNVolume is the volume of Body N.
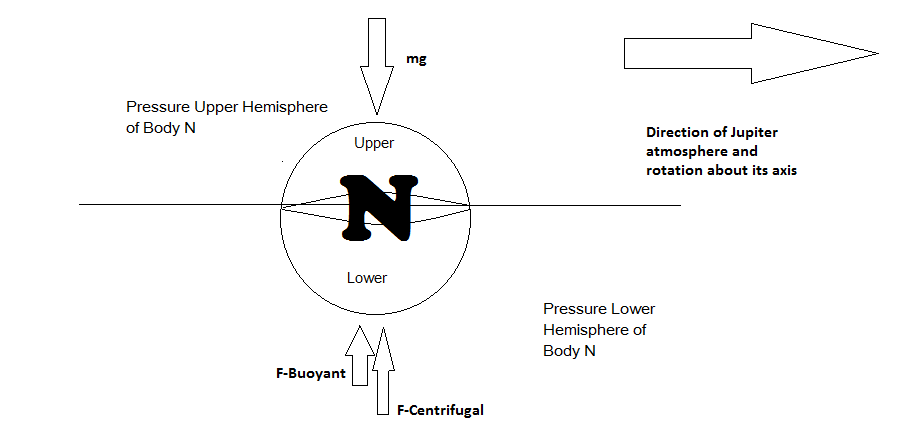
Buoyancy is actually a reality due to pressure differences in the fluid from lower to higher depths. A better model for FBuoyant for Body N will account for the extreme pressure differences in Jupiter's atmosphere. We know that Pressure = Force / Area and that Force due to Pressure, F = Pressure * Area.
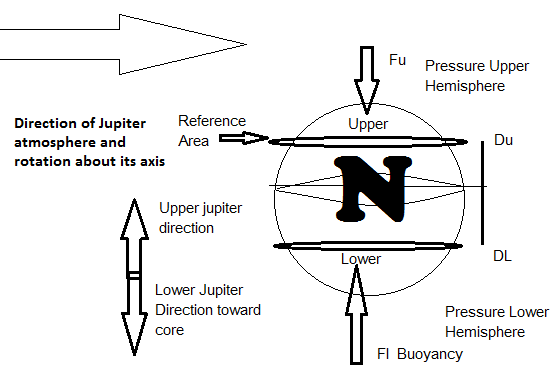
We will break down the FBuoyant force for modeling reasons into FBU (upper hemisphere) and FBL (lower hemisphere) to represent the Net buoyant forces due to pressure in the upper and lower hemispheres of Body N.
FBuoyant = FBL - FBU
FBuoyant = PL* AL - PU*AU,
where PL corresponds to lower hemisphere pressure, PU corresponds to the pressure surrounding upper hemisphere, AL and AU are area at Pi*(Radius)2.
Simplifying math and substiting for the pressures based on the above fluid pressure illustration yields
Large Body Pressure Model for Buoyant forces
FBuoyant ~ A*rho*g*(DL - DU),
where A is Pi*(Radius)2 , rho is density of surrounding Jupiter atmosphere, g is gravity of Jupiter, DL and DU are the depth distances for the modeling of lower and upper hemispheres of body N with respect to Jupiter's geometric center.
As you can see the Buoyant force on Body N can have significant magnitude depending on the modeling assumptions. Each 1000 km of Jupiter's Atmosphere creates a pressure difference on the order of 1.74 X 109 N/m2 with these current assumptions.
Drive Force on Body N
FD ~ (rho * VF2)A/2,
where rho is the density of the fluid, VF is the speed of the fluid with respect to Body N, and A is the flow facing reference area. The typical model for flow force on a body is illustrated below.
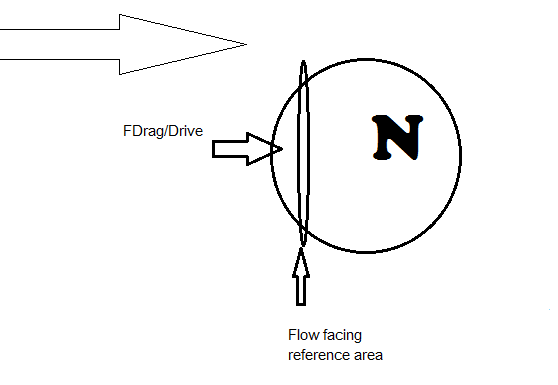
For more accurate modeling and the significant size of both Body N and Jupiter's flowing atmosphere we can further refine this drive force due to fluid velocity. If we consider the flow facing quadra spheres of Body N as illustrated below, the lower drive force and upper drive forces can be separated. We will see that the FDrive on Body N has a gravity canceling result or component in the up direction due to upper and lower hemispheric pressures.
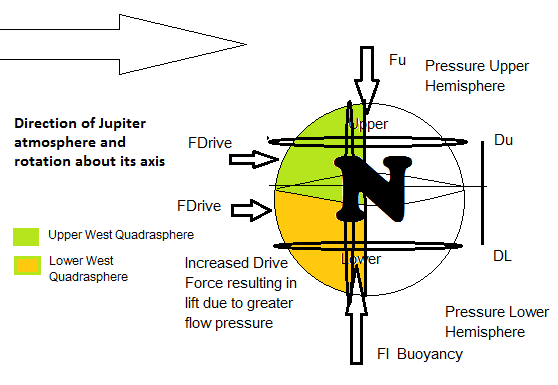
The green and orange quadra spheres represent the reference areas for drive force due to Jupiter's atmosphere. The resultant force on the body due to flow is under the center of mass rather than direct at the front facing center of mass when you consider large bodies.
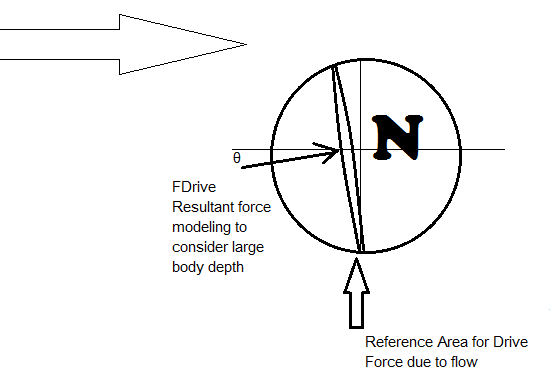
Using this modeling for FDrive we get
FDrive ~ ((rho * VF2)A/2) cos(Ø) in the prograde direction & ((rho * VF2)A/2) sin(Ø) in the radially out direction from Jupiter center
Where Ø is determined by the pressure difference between the upper and lower hemispheres of Body N.
Ø ~ (PL - PU)/PL ,
Where Ø refers to the resultant force angle and direction and is dependent on the pressures in the fluid atmosphere around it. These pressures as shown above depend on the size on Body N, gravity, and momentums near Body N.
Body N is riding a persistent fluid pressure wave much similar to a surfer at the beach due to the large pressure differences and momentum.
Summation of Net forces on Body N
Forces in the prograde direction are primarily due to fluid velocities on the compressed Jupiter atmosphere. As seen from above we can model this FDrive force as:
FDrive ~ ((rho * VF2)A/2) cos(Ø)
Forces up and down along the radial direction of Jupiter include gravity and fluid buoyancy modeling as seen from above. The summation of forces in the radial direction for Body N are:
FNetRadial ~ FBuoyant + FDriveR + FCentrifugal - MNgJ, where
FBuoyant ~ A*rho*g*(DL - DU),
FDriveR ~ ((rho * VF2)A/2) sin(Ø)
FCentrifugal ~ MN * ca (centrifugal acceleration based on speed, on the order of 2 m/s2
and MN refers to the mass of Body N, gJ refers to Jupiter gravity strength, and ca refers to the centrifugal accelerations as calculated below.
Jupiter's Suggested Gravity with the Knowledge of Body N
Given that Body N is significant in size and mass Body N also contains a gravity field of its own. If you consider planetary neighbors we could estimate Body N to be on the order of 2500 km in radius and have a mass on the order of 1 X 1023 kg. Given this significant size and mass Body N must have a significant effect on and within Jupiter's gravity field.
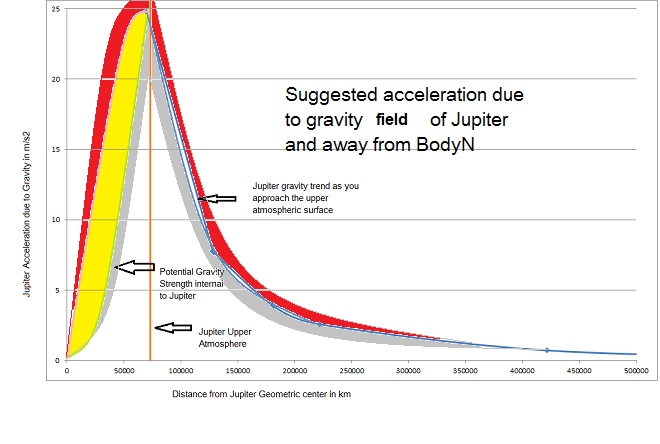
The plot above is a suggested gravity model for Jupiter radially along its equitorial middle. The model includes the presence of a significant Body N. Close approach gravity measurement around Jupiter's equator may see a noticeable field variation directly over Body N. The RED regions in the above plot indicate the strength in the presence of Body N and GRAY regions represent the lower gravity strength in the absence of Body N.
Body N can arguably feel the pull of its gravity neighbors including the Galilean moons. As Body N orbits internally to Jupiter's atmosphere it is part of Jupiter's gravity interaction each time a fellow moon passes. As Body N orbits internally at high altitudes its gravity interaction and noticeable effects become greater with time. A Body N with more mass would effect the gravity field by more.
We look at some neighbors for magnitudes of potential Body N characteristics.
Body N Neighbors |
Io |
Europa |
Ganymede |
Callisto |
Mars |
Earth |
| Equatorial Radius km | 1821 km | 1,560 km | 2,631 km | 2,410 km | 3,389 km | 6,371 km |
| Mass kg | 8.9319 x 1022 kg | 4.7998 x 1022 kg | 1.4819 x 1023 kg | 1.0759 x 1023 kg | 6.4169 x 1023 kg | 5.9722 x 1024 kg |
| Density kg/m3 | 3528 kg/m3 | 3013 kg/m3 | 1942 kg/m3 | 1834 kg/m3 | 3934 kg/m3 | 5513 kg/m3 |
| Gravity | 1.796 m/s2 | 1.315 m/s2 | 1.428 m/s2 | 1.236 m/s2 | 3.71 m/s2 | 9.8 m/s2 |
| Volume | 25,319,064,907 km3 | 15,926,867,918 km3 | 76,304,506,998 km3 | 58,654,577,603 km3 | 163,115,609,799 km3 | 1,083,206,916,846 km3 |
| Fluid Drag Reference Area in km2 | 10,417, 641 km2 | 7,645,373 km2 | 21,746,591 km2 | 18,246,668 km2 | 36,082,169 km2 | 127,516,010 km2 |
Analysis of the Great Red Spot of Jupiter
The great red spot of Jupiter is often times referred to as a storm similar to a hurricane here on Earth. However this storm and the great read spot have been visible on Jupiter for hundreds of years. The spot is observed and apparent just below the equator in Jupiter's Southern hemisphere. The size of this spot has decreased over the years however is larger than the planet Earth.
The Great Red Spot is seen to orbit about Jupiter at roughly the speed planet rotates while spinning in the upper jet streams. As you can see from the pressure and thermal flow compositions of Jupiter that eddys and swirls are possible. Specifically when you see the separation lines in Jupiter's upper Jet Streams.
As you can see from the significant size of pressure differences and fast thermal fluid flows in Jupiter's upper atmosphere a significant Body N would cause a funnel cloud with tight enough spin to reach the outer atmosphere.
While Body N is persistently being driven by the atmosphere around it, Body N is large enough and close enough to the upper equatorial atmosphere to maintain a steady and persistent vortex in its wake.
This spiraling vortex presents itself as the great read spot of Jupiter.
Purpose of Gravity
The purpose of gravity is to bring and keep mass together. Mass is moved by gravity and moves in spite of gravity. However, mass cannot ignore gravity unless it escapes it.



